SIFEL (SImple Finite ELements) is an open-source computer finite element (FE) code that has been developed since 2001 at the Department of Mechanics of the Faculty of Civil Engineering of the Czech Technical University in Prague. It is C/C++ code parallelized with MPI. Developers requested a POP performance assessment of the PARGEF module containing the Schur complement method.

In the initial audit, we identified the structure and hotspots of the application. It performs a matrix factorization followed by an iterative solver. Besides an issue with load balance caused by a non-uniform mesh distribution, we came to the conclusion that the matrix factorization implementation is not efficient as it takes a disproportionate amount of time and more than 90 % of the runtime. Since the matrix factorization and the Schur complement computation is a well-studied mathematical and algorithmic problem that was already implemented in many math libraries, we decided to replace the original implementation by a call to the Pardiso library that is a part of the Math Kernel Library (MKL).

A system matrix in the original code was stored in symmetric skyline format and it was then factorized. For the Pardiso library, we stored the matrix into compressed sparse row (CSR) format trying both variants, general and symmetric matrix format. We prepared the appropriate interface for the Pardiso library and computed the factorization.

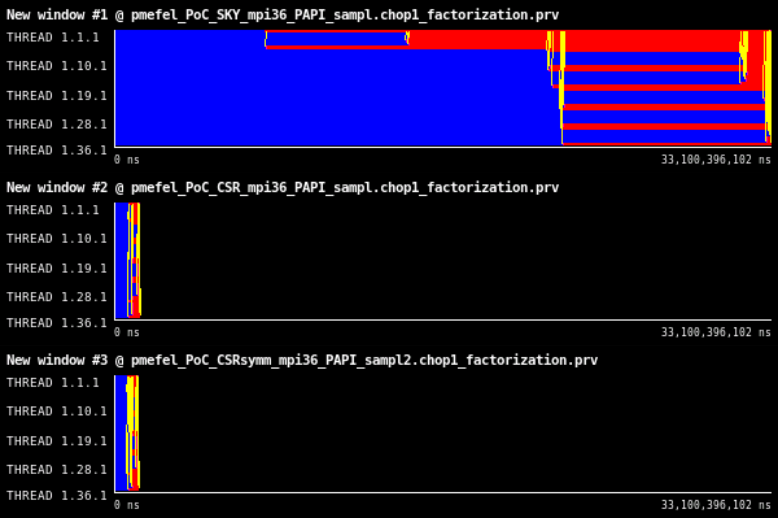
Figure 1: Traces of the original factorization with symmetric skyline matrix format, MKL factorization with general CSR matrix format, and MKL factorization with symmetric CSR matrix format.

In Figure 1, we can see the difference between the original implementation and the implementation within the Pardiso library (MKL). Application runtime is on the x-axis and individual processes are on the y-axis. Black is idle corresponding to the end of the application, other colors indicate various states, where blue is a computation, red is synchronization or communication. By the yellow lines, the communication flow is depicted. On the tested case, where the input matrix is of size ~45Kx45K with ~800K nonzero elements and the size of the Schur complement matrix varies from 600 to 1200 across 36 MPI processes on a single node of the Barbora cluster at IT4Innovations Supercomputing Center, the speedup is 27.81 and 29.65 for general and symmetric matrix, respectively.

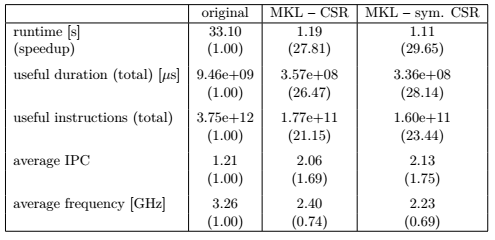
Table 1: Overview of the runtime, total useful duration, total useful instructions, IPC, and frequency with the relative ratio to the original code stated in brackets.

An explanation for the speedup when using the MKL library instead of the original implementation can be found in Table 1. The main reason is the reduction of instructions. When adding also higher average IPC and lower frequency that is probably caused by utilizing vector instructions, we obtain the measured speedups.

-- Lukáš Malý (IT4I)